CONJUNTO

1-En matemáticas, un conjunto es una colección de elementos considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser las siguientes: personas, números, colores, letras, figuras, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.

2-Un conjunto se define como la agrupación de diferentes elementos que comparten entre sí características y propiedades semejantes. Estos elementos pueden ser cualquier cosa, tales como números, canciones, meses, personas, etcétera.

3-Un conjunto es la agrupación, clase, o colección de objetos o en su defecto de elementos que pertenecen y responden a la misma categoría o grupo de cosas, por eso se los puede agrupar en el mismo conjunto. Esta relación de pertenencia que se establece entre los objetos o elementos es absoluta y posiblemente discernible y observable por cualquier persona.

https://www.definicionabc.com/general/conjunto.php

DIAGRAMA DE VENN

¿Qué es?

1- Un diagrama de Venn usa círculos que se superponen u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos. A menudo, se utilizan para organizar cosas de forma gráfica, destacando en qué se parecen y difieren los elementos. Los diagramas de Venn, también denominados "diagramas de conjunto" o "diagramas lógicos", se usan ampliamente en las áreas de matemática, estadística, lógica, enseñanza, lingüística, informática y negocios.

Resultado de imagen para ejemplos de diagrama de venn

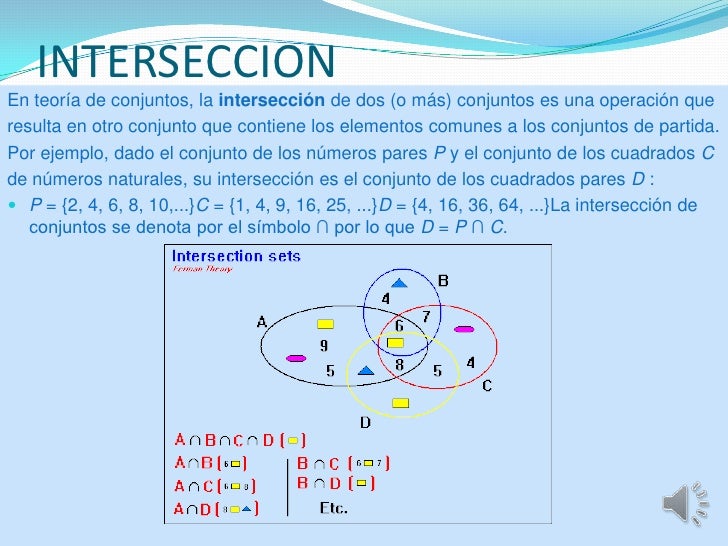
Resultado de imagen para operaciones basicas de conjunto

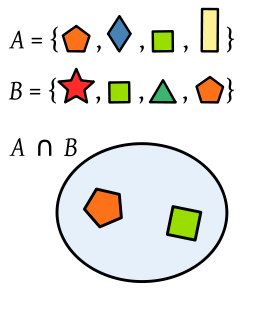
Intersección de conjuntos

Ir a la navegación Ir a la búsqueda

En teoría de conjuntos, la intersección de dos (o más) conjuntos es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. Por ejemplo, dado el conjunto de los números pares $P$ y el conjunto de los cuadrados $C$ de números naturales, su intersección es el conjunto de los cuadrados pares D:

P=\{2,4,6,8,10,\ldots \}

C=\{1,4,9,16,25,\ldots \}

D=\{4,16,36,64,\ldots \}

En otras palabras: Así, por ejemplo, si A = { a, b, c, d, e, f} y B = { a, e, i, o, u}, entonces la intersección de dichos conjuntos estará formada por todos los elementos que estén a la vez en los dos conjuntos, esto es: A $\cap$ B = { a, e}

La intersección de conjuntos se denota por el símbolo $\cap$ por lo que $D = P \cap C$ .

PROBLEMAS

De una encuesta hecha a 135 personas para establecer preferencias de lectura de las revistas A, B y C; se obtienen los siguientes resultados: Todos leen alguna de las 3 revistas; todos, menos 40, leen A; 15 leen A y B pero no C, 6 leen B y C pero no A; 10 leen sólo C. El número de los que leen A y C es el doble del número de los que leen las 3 revistas. El número de los que leen sólo B es el mismo que el total de los que leen A y C. Según todo esto, hallar el número de los que leen solamente A.

De un grupo de 62 trabajadores, 25 laboran en lafábrica A, 33 trabajan en la fábrica B, 40 laboran en la fábrica C y 7 trabajadores están contratados en las tres fábricas. ¿Cuántas personas trabajan en dos de estas fábricas solamente?

Diferencia

La diferencia entre dos conjuntos $A$ y $B$ es el conjunto $A \ B$ que contiene todos los elementos de $A$ que no pertenecen a $B.$

Diferencia simétrica

La diferencia simétrica entre dos conjuntos $A$ y $B$ es el conjunto que contiene los elementos de $A$ y $B$ que no son comunes.

En teoría de conjuntos, la diferencia simétrica de dos conjuntos es una operación que resulta en otro conjunto cuyos elementos son aquellos que pertenecen a alguno de los conjuntos iniciales, sin pertenecer a ambos a la vez. Por ejemplo, la diferencia simétrica del conjunto de los números pares $P$ y el conjunto de los cuadrados perfectos $C$ es un conjunto $D$ que contiene los cuadrados impares y los pares no cuadrados:

$P=\{2,4,6,8,10,12,14,16,\ldots \}$

$C=\{1,4,9,16,25,\ldots \}$

$D=\{1,2,6,8,9,10,12,14,18,\ldots \}$

La diferencia simétrica de conjuntos se denota por $Δ$ , por lo que $P Δ C = D$

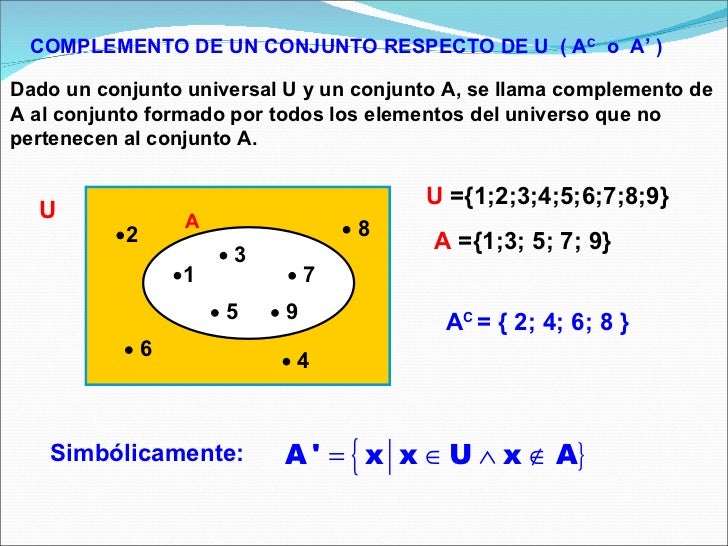
Complemento

El complemento de un conjunto $A$ es el conjunto $A ∁$ que contiene todos los elementos que no pertenecen a $A$ .

El complemento de un conjunto o conjunto complementario es otro conjunto que contiene todos los elementos que no están en el conjunto original. Para poder definirlo es necesario especificar qué tipo de elementos se están utilizando, o de otro modo, cuál es el conjunto universal. Por ejemplo, si se habla de números naturales, el complementario del conjunto de los números primos $P$ es el conjunto de los números no primos $C$ , que está formado por los números compuestos y el 1:

$\mathbf {P} =\{2,3,5,7,\ldots \}$

$C=\{1,4,6,8,9,\ldots \}$

A su vez, el conjunto $C$ es el complementario de $P$ . El conjunto complementario se denota por una barra horizontal o por el superíndice « $∁$ », por lo que se tiene: $P ∁ = C$ , y también $C = P$ .

El conjunto complementario de $A$ es la diferencia (o complementario relativo) entre el conjunto universal y $A$ , por lo que ambas operaciones (complementario y diferencia) tienen propiedades similares.

Producto cartesiano

El producto cartesiano de dos conjuntos $A$ y $B$ es el conjunto $A \times B$ que contiene todos los pares ordenados (a, b) cuyo primer elemento pertenece a $A$ y su segundo elemento pertenece a $B$ .

En matemáticas, el producto cartesiano de dos conjuntos es una operación, que resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse de forma que el primer elemento del par ordenado pertenezca al primer conjunto y el segundo elemento pertenezca al segundo conjunto.

Por ejemplo, dados los conjuntos:

$A=\{1,2,3,4\}$

y

$B=\{a,b\}$

su producto cartesiano es:

${\begin{array}{r|cccc}b&(1,b)&(2,b)&(3,b)&(4,b)\\a&(1,a)&(2,a)&(3,a)&(4,a)\\\hline A\times B&1&2&3&4\\\end{array}}$

que se representa:

$A\times B=\{(1,a),(1,b),(2,a),(2,b),(3,a),(3,b),(4,a),(4,b)\}$

El producto cartesiano recibe su nombre de René Descartes, cuya formulación de la geometría analítica dio origen a este concepto.