COMBINATORIA

                                                         COMBINATORIA 

La combinatoria es una rama de la matemática perteneciente al área de matemáticas discretas  que estudia la enumeración, construcción y existencia de propiedades de configuraciones que satisfacen ciertas condiciones establecidas. Además, estudia las ordenaciones o agrupaciones de un determinado número de elementos.

https://es.wikipedia.org/wiki/Combinatoria.

Los números combinatorios se utilizan para establecer agrupaciones en las que no importa el orden y los elementos no se pueden repetir, es decir, para calcular directamente las combinaciones. Se representan así: , y se lee "n sobre p". 

https://www.um.es/documents/14554/1639495/5-Materiales-apoyo-Combinatoria_.pdf/101efa8c-442e-43cd-a452-dc3839278773

La combinatoria es una sección de las matemáticas que resulta útil para diversos representantes de variadas especialidades.Con los problemas combinatorios deben representarse los biólogos. físicos, los matemáticos lingüísticos ingenieros y muchos otros usuarios.  

El estudio de la combinatoria constituye la base de contiene la base y solución de muchos problemas relacionados con la teoría y de las probabilidades y sus aplicaciones. 

https://es.slideshare.net/verdugo87/combinatoria-13090451

La combinatoria, el estudio de las posibles distribuciones de objetos, es una parte importante de la matematica discreta, que ya era estudiada en el siglo XVII, ´epoca en la que se plantearon cuestiones combinatorias, relacionadas principalmente con los juegos de azar.

http://www.dma.fi.upm.es/docencia/grado_ii/matematica_discreta_1/resumen/tecnicas_contar.pdf

                                            COMBINATORIA CON REPETICIÓN 

Las combinaciones con repetición de m elementos tomados de n en n (m ≥ n), son los distintos grupos formados por n elementos de manera que:

No entran todos los elementos.

No importa el orden.

Sí se repiten los elementos.

                                                      PERMUTACIÓN 

En matemáticas, una permutación es la variación del orden o de la disposición de los elementos de un conjunto ordenado  o una tupia sin elementos repetidos.

Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para conjuntos de 3 elementos, en este caso: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".

https://es.wikipedia.org/wiki/Permutaci%C3%B3n

Es una noción que proviene del latín permutatio. El término refiere al procedimiento y el resultado de permutar. Este verbo, por su parte, hace mención al canje de una cosa por otra, sin la intermediación de dinero a menos que se busque equiparar el valor de los objetos permutados.

https://definicion.de/permutacion/

                                               PERMUTACIÓN CON REPETICIÓN 

Las permutaciones con repetición de  elementos en las que el primer elemento se repite veces, el segundo  veces, ... y el último se repite  veces, son los distintos grupos de elementos que se pueden hacer de forma que en cada grupo, cada elemento aparezca el número de veces indicado. Además, dos grupos se diferencian únicamente en el orden de la colocación. Se representa por.

https://www.sangakoo.com/es/temas/permutaciones-con-repeticion.

Permutaciones con repetición de n elementos en las que el primer elemento se repite n₁ veces, el segundo se repite n₂ veces ... y el último se repite  n_k veces son los distintos grupos de n elementos que se pueden hacer de forma que en cada grupo, cada elemento aparezca el número de veces indicado y que dos grupos se diferencian únicamente en el orden de colocación. Se representa por P_n^{n1,n2,...,nk.}

http://recursostic.educacion.es/descartes/web/materiales_didacticos/Combinatoria/permutacionescon.htm


Combinatio, combinación es una palabra que refiere al acto y consecuencia de combinar algo o de combinarse(es decir, unir, complementar o ensamblar cosas diversas para lograr un compuesto). El concepto posee múltiples aplicaciones ya que las cosas factibles de combinar son de características y orígenes muy 
diversos.

https://definicion.de/combinacion/


Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
http://www.aaamatematicas.com/sta-combin.htm



   

                                                COMBINACIÓN CON REPETICIÓN 

• Una ficha de dominó es un rectángulo en el que hay dos partes, en cada una de ellas hay una serie de puntos que indican la puntuación de esa parte. Estas puntuaciones van de blanca (0 puntos) a 6. Tenemos pares de puntuaciones de 0 a 6.
El total de fichas será 

• En una pastelería hay 6 tipos distintos de pasteles. ¿De cuántas formas se pueden elegir 4 pasteles?.

Nota: Si nos gusta un pastel lo podemos pedir hasta cuatro veces.
Estamos en el caso en el que no nos importa el orden en que elijamos los pasteles y podemos repetir, son combinaciones con repetición.

• En una bodega hay en un cinco tipos diferentes de botellas. ¿De cuántas formas se pueden elegir cuatro botellas?
  No entran todos los elementos. Sólo se seleccionan 4. No importa su orden y se puede elegir más de una botella del mismo tipo. Podemos resolver este problema de esta forma: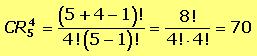
  
• en una heladería tienen se venden helados en los que se pueden elegir entre dos sabores que se pueden repetir, ¿cuántos helados de sabores diferentes podemos elegir entre los sabores de nata, vainilla, chocolate, limón y naranja?

m = 5 sabores diferentes

n = 2 (helados de dos sabores)

CR_mⁿ = CR₅² = (5 + 2 - 1)! / [2! (5-1)!] = 6! / (2! · 4!) = (6 · 5 · 4 · 3 · 2 · 1) / (2 · 1 · 4 · 3 · 2 · 1) = 15 combinaciones

 http://www.ugr.es/~jesusgm/Curso%202005-2006/Matematica%20Discreta/Combinatoria.pdf

 En el sistema de matriculación vigente cada matrícula se compone de cuatro dígitos y tres consonantes (salvo la "Ñ"). Si consideramos los conjuntos D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} C = {B, C, D, F, G, H, J, K, L, M, N, P, Q, R, S, T, V, W, X, Y, Z} cada matrícula puede identificarse entonces con un elemento de D × D × D × D × C × C × C cuyo cardinal es 104 · 213 = 92610000 (existe una biyección entre el conjunto de posibles matrículas y D × D × D × D × C × C × C)

                                 PERMUTACIONES CON REPETICIÓN 

• En una urna hay 9 bolas, 3 blancas, 2 rojas y 4 negras. ¿De cuantas formas distintas se pueden extraer las bolas de la urna?

Al tener tres bolas blancas, a efectos de ordenación se consideran iguales, lo mismo ocurre con las rojas y las negras.
Las posibles ordenaciones son: 

• En una competición deportiva participan 4 equipos de 3 atletas cada uno. ¿De cuántas formas diferentes pueden llegar los equipos?
A la hora de elaborar la clasificación por equipos los atletas se consideran idénticos.
El número de posibles clasificaciones es: .
• Con las letras de la palabra BALADA, tenemos que averiguar cuántas palabras distintas se pueden formar, que tengan o no sentido.

Date cuenta que los grupos que se pueden formar, es decir, cada palabra, se diferencian por el criterio de orden, luego se trata de permutaciones y además con repetición, ya que la A está repetida tres veces.

P36 = 6!/3! = (6·5·4·3·2·1)/(3·2·1) = 120 palabras

• ¿Cuántos números de siete cifras se pueden formar con dos 3, cuatro 5 y un 6?

Estamos ante un claro caso de combinaciones con repetición. Son permutaciones porque los grupos de números nada más que se diferencian por el criterio de orden y con repetición por tener cada grupo elementos repetidos.

P2,47 = 7!/2!4! = (7·6·5·4·3·2·1)/(2·1·4·3·2·1) = 105 números

Cuántos números mayores que 100000 se pueden escribir con las  cifras 0, 3, 3, 4, 5, 6?

Podremos formar:

P26 = (6·5·4·3·2·1)/(2·1) = 360 números

Pero debemos recordar que cuando el 0 vaya delante de todos, los números que se formen así no son mayores de 100000, es decir de 6 cifras, sino menores de 100000, es decir, de 5 cifras, que se formarán con las cifras 3, 3, 4, 5, 6.

P25 = (5·4·3·2·1)/(2·1) = 60 números

Por lo tanto, la cantidad de números que se pueden formar con las cifras 0, 3, 3, 4, 5, 6 mayores que 100000 es:

360 – 60 = 300 números

https://eluniversomatematicoblog.wordpress.com/2017/09/22/ejemplos-de-permutaciones-con-repeticion/